Central Probability in a Normal or T Distribution

Source: R/xpnorm.R

These versions of the quantile functions take a vector of central probabilities as its first argument.

cnorm(p, mean = 0, sd = 1, log.p = FALSE, side = c("both", "upper", "lower"))

ct(p, df, ncp, log.p = FALSE, side = c("upper", "lower", "both"))

Arguments

p

vector of probabilities.

mean

vector of means.

sd

vector of standard deviations.

log.p

logical; if TRUE, probabilities p are given as log(p).

side

One of "upper", "lower", or "both" indicating whether a vector of upper or lower quantiles or a matrix of both should be returned.

df

degrees of freedom (\(> 0\), maybe non-integer). df = Inf is allowed.

ncp

non-centrality parameter \(\delta\); currently except for rt(), only for abs(ncp) <= 37.62. If omitted, use the central t distribution.

Examples

qnorm(.975)
#> [1] 1.959964
cnorm(.95)
#>          lower    upper
#> [1,] -1.959964 1.959964
xcnorm(.95)
#> 
#> If X ~ N(0, 1), then 
#> 	P(X <= -1.959964) = 0.025	P(X <=  1.959964) = 0.975
#> 	P(X >  -1.959964) = 0.975	P(X >   1.959964) = 0.025
#> 

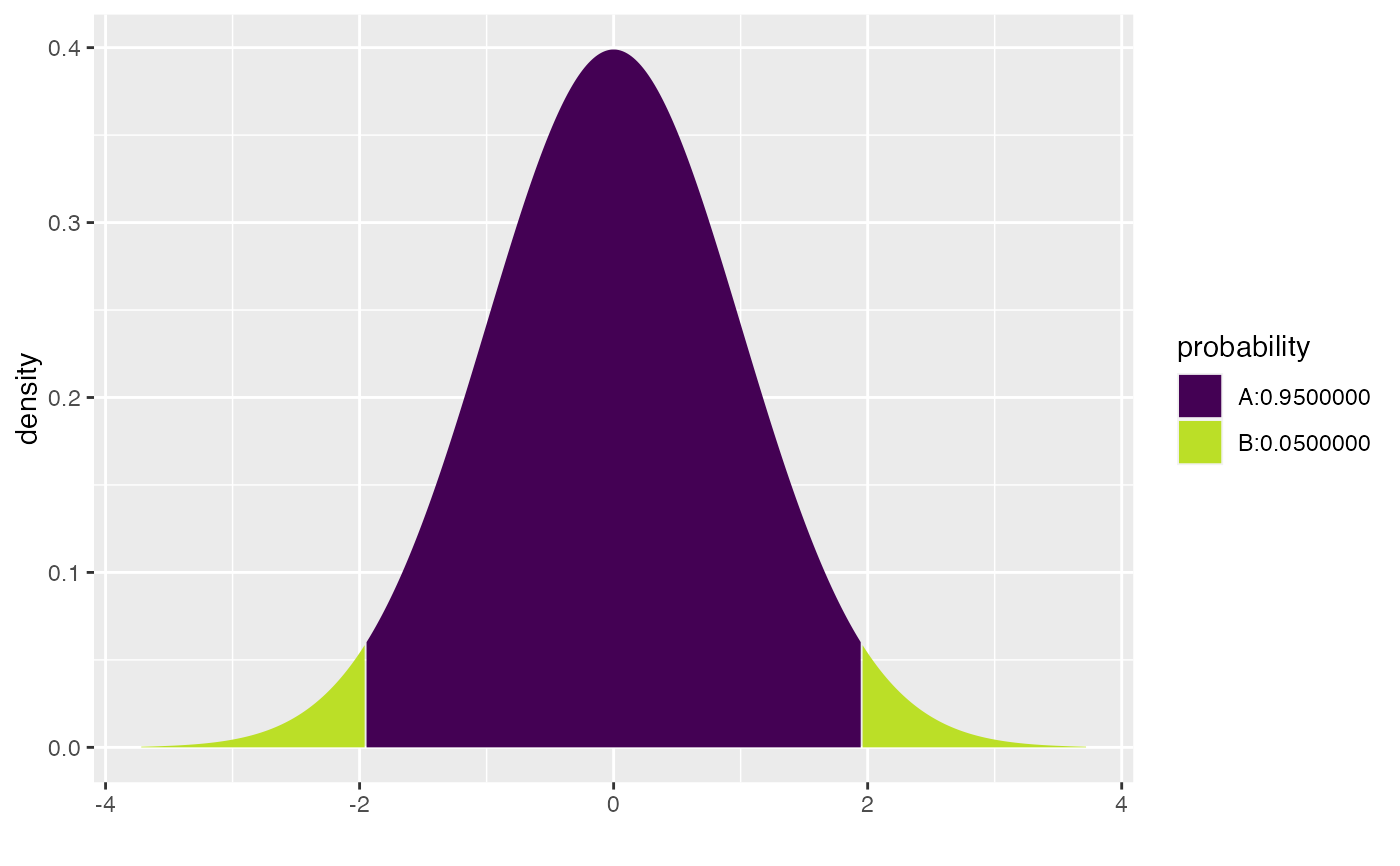#> [1] -1.959964  1.959964
xcnorm(.95, verbose = FALSE, return = "plot") %>%
  gf_refine(
  scale_fill_manual( values = c("navy", "limegreen")),
  scale_color_manual(values = c("black", "black")))
#> Scale for 'fill' is already present. Adding another scale for 'fill', which
#> will replace the existing scale.
#> Scale for 'colour' is already present. Adding another scale for 'colour',
#> which will replace the existing scale.

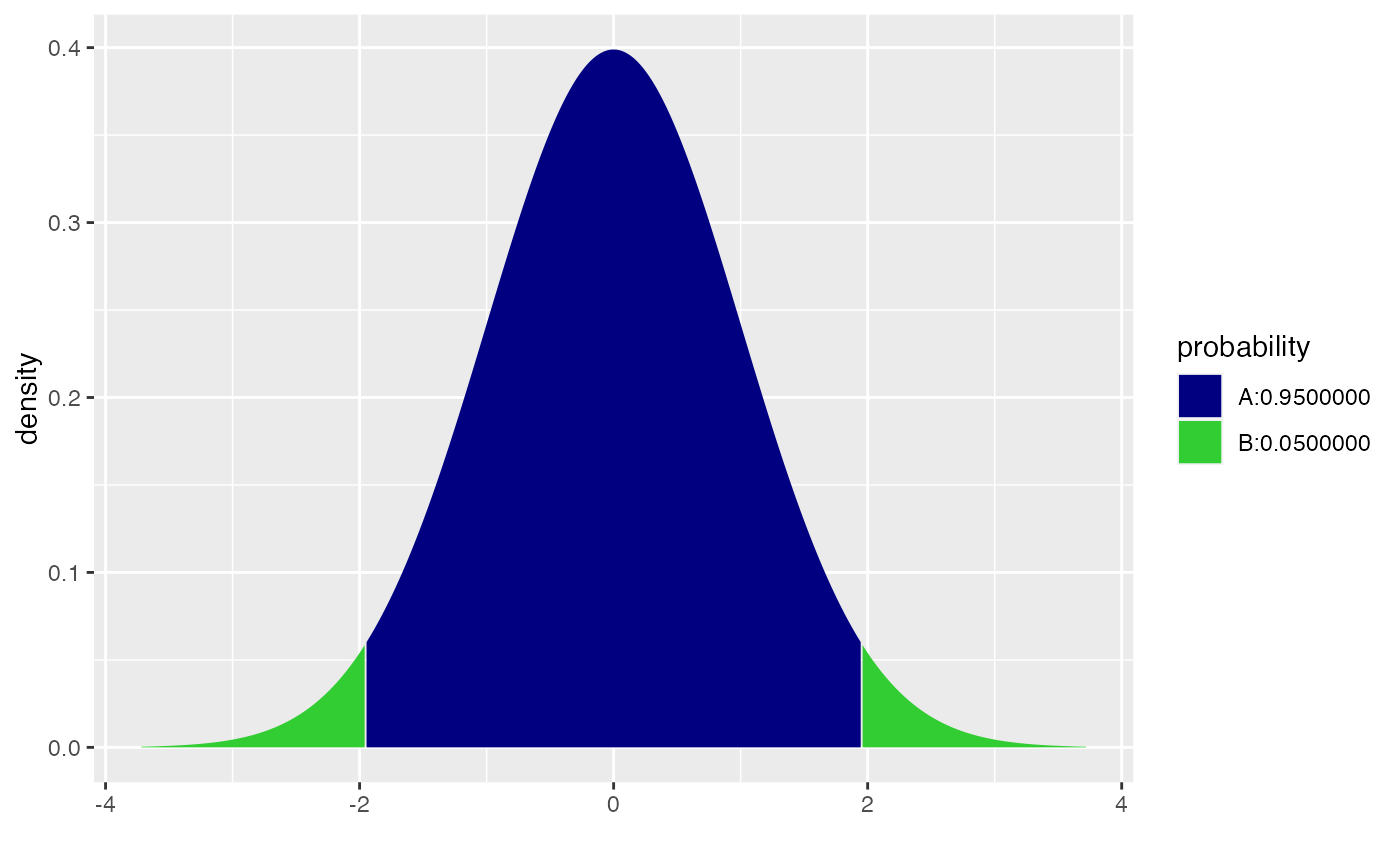cnorm(.95, mean = 100, sd = 10)
#>         lower    upper
#> [1,] 80.40036 119.5996
xcnorm(.95, mean = 100, sd = 10)
#> 
#> If X ~ N(100, 10), then 
#> 	P(X <=  80.40036) = 0.025	P(X <= 119.59964) = 0.975
#> 	P(X >   80.40036) = 0.975	P(X >  119.59964) = 0.025
#> 

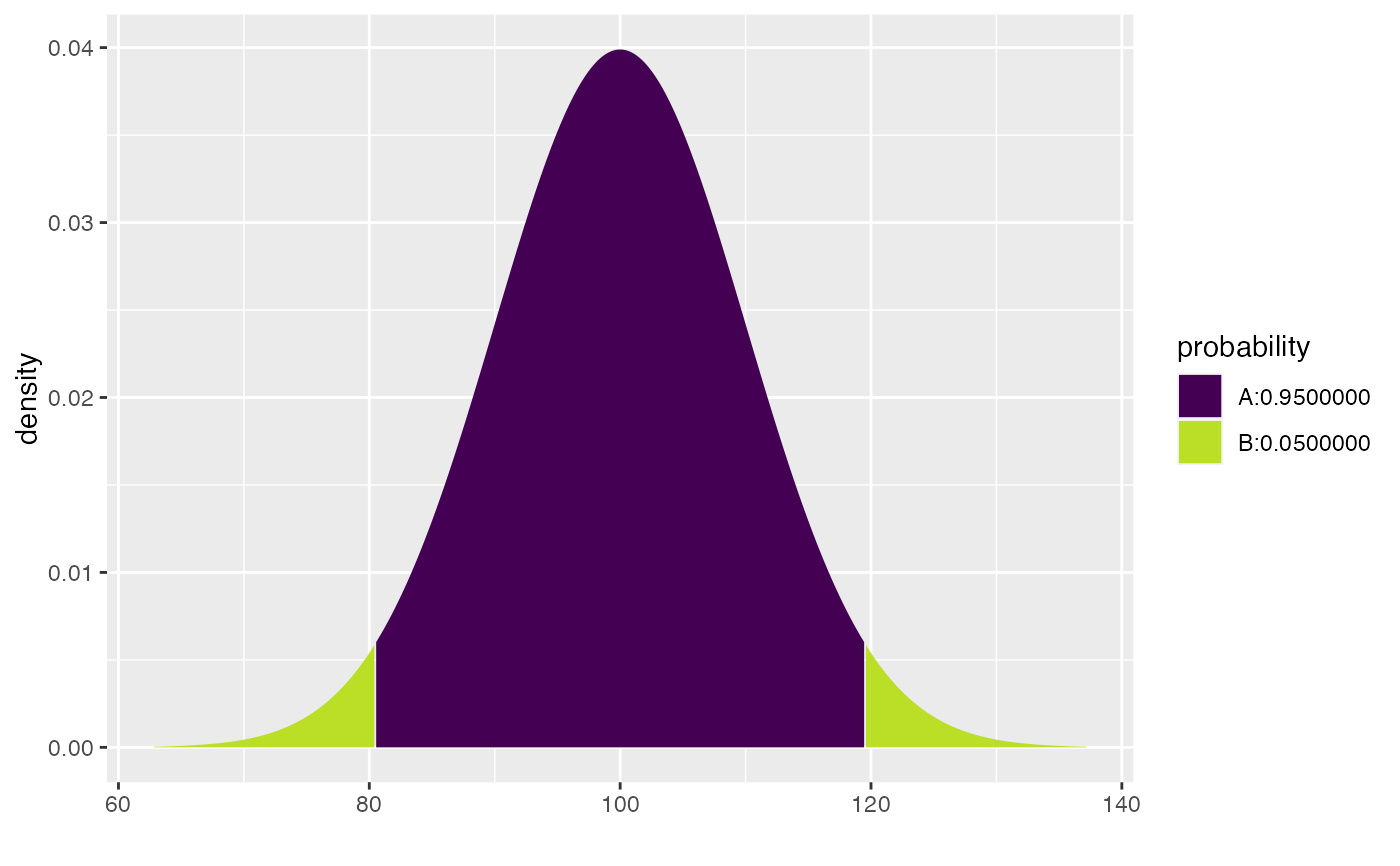#> [1]  80.40036 119.59964