28 Vectors
Until now, our encounter with functions has been via formulas relating inputs to an output. Now we turn to a different way of representing functions: columns of numbers that we call vectors. The mathematical notation for the name of a vector shows the name surmounted with an arrow, for instance, \(\vec{u}\).
The columns-of-numbers framework is central to technical work in many fields. For instance, an algorithm in this framework was the spark that ignited the modern era of search engines. The name given to it by mathematicians is linear algebra, although only the word “linear” conveys helpful information about the subject. (The physicists who developed the first workable quantum theory called it matrix mechanics. A matrix is a collection of vectors.)
Although the words “algebra” and “quantum” may suggest that conceptual difficulties are in store, human intuition is well suited to establishing an understanding. In this book, we use two intuitive formats to introduce linear algebra: (1) geometric and visual and (2) simple arithmetic.
28.1 Length & direction
A vector is a mathematical idea deeply rooted in everyday physical experience. Geometrically, a vector is simply an object consisting only of length and direction.
A pencil is a physical metaphor for a vector, but a pencil has other non-vector qualities such as diameter, color, and an eraser. And, being a physical object, a pencil has a position in space.

A line segment has an orientation but no forward or backward direction. In contrast, a vector has a unique direction: like an arrow, one end is the tip and the other the tail. In the pencil metaphor, the writing end is the tip; the eraser is the tail.

Vectors are always embedded in a vector space. Our physical stand-ins for vectors, the pencils, were photographed on a tabletop: a two-dimensional space. Naturally, pencils are embedded in everyday three-dimensional space. (The tabletop is a kind of two-dimensional subspace of three-dimensional space.)
Vectors embedded in three-dimensional space are central to physics and engineering. Quantities such as force, acceleration, and velocity are not simple numerical quantities but vectors with magnitude (that is, length) and direction. For instance, the statement, “The plane’s velocity is 450 miles per hour to the north-north-west,” is perfectly intelligible to most people, describing magnitude and direction. Note that the plane’s velocity vector does not specify the plane’s location; vectors have only the two qualities of magnitude and direction.
The gradients that we studied with partial differentiation (Chapter 24) are vectors. A gradient’s direction points directly uphill; its magnitude tells how steep the hill is.
Vectors often represent a change in position, that is, a step or displacement in the sense of “step to the left” or “step forward.” As we will see, constructing instructions for reaching a target is a standard mathematical task. Such instructions have a form like, “take three and a half steps along the green vector, then turn and take two steps backward along the yellow vector.” An individual vector describes a step of a specific length in a particular direction.
Vectors are a practical tool to keep track of relative motion. For instance, consider the problem of finding an aircraft heading and speed to intercept another plane that is also moving. The US Navy training movie from the 1950s shows how to perform such calculations with paper and pencil.
Nowadays, the computer performs such calculations. On the computer, vectors are represented not by pencils (!) but by columns of numbers. For instance, two numbers will do for a vector embedded in two-dimensional space and three for a vector embedded in three-dimensional space. From these numbers, simple arithmetic can produce the vector magnitude and direction.
Representing a vector as a set of numbers requires the imposition of a framework: a coordinate system. In Figure 28.3, the vector (shown by the green pencil) lies in a two-dimensional coordinate system. The two coordinates assigned to the vector are the difference between the tip and the tail along each coordinate direction. In the figure, there are 20 units horizontally and 16 units vertically, so the vector is \((20, 16)\).

By convention, when we write a vector as a set of coordinate numbers, we write the numbers in a column. For instance, the vector in Figure 28.3, which we will call \(\vec{green}\), is written numerically as:
\[\vec{green} \equiv \left[\begin{array}{c}20\\16\end{array}\right]\]
In more advanced linear algebra, the distinction between a column vector (like \(\vec{green}\)) and a row vector (like \(\left[20 \ 16\right]\)) is important. For our purposes in this block, we need only column vectors.
Construct column vectors with the rbind() function, as in
green <- rbind(20, 16)Commas separate the arguments—the coordinate numbers—in the same way as any other R function.
Later in this block, we will use data frames to define vectors. We will introduce the R syntax for that when we need it.
In physics and engineering, vectors describe positions, velocities, acceleration, forces, momentum, and other functions of time or space. In mathematical notation, a vector-valued function can be written \(\vec{v}(t)\). It is common to perform calculus operations such differentiation, writing it as \(\partial_t \vec{v}(t)\). It is sometimes easier to grasp a vector-valued function by writing it as a column of scalar-valued functions: \[\vec{v}(t) = \left[\begin{array}{c}v_x(t)\\v_y(t)\\v_z(t)\end{array}\right]\] where the \(x\), \(y\), and \(z\) refer to the axes of the coordinate system.
28.2 The nth dimension
In many applications, especially those involving data, vectors have more than three components. Indeed, you will soon be working with vectors with hundreds of components. Services like Google search rely on vector calculations with millions of vectors, each having millions of components.
Living as we do in a palpably three-dimensional space and with senses and brains evolved for use in three dimensions, it is hard and maybe even impossible to grasp high-dimensional spaces.
A lovely 1884 book, Flatland features the inhabitants of a two-dimensional world. The central character in the story, named Square, receives a visitor, Sphere. Sphere is from the three-dimensional world which embeds Flatland. Only with difficulty can Square assemble a conception of the totality of Sphere from the appearing, growing, and vanishing of Sphere’s intersection with the flat world. (Among other things, Flatland is a parody of humanity’s rigid thinking: Square’s attempt to convince Sphere that his three-dimensional world might be embedded in a four-dimensional one leads to rejection and disgrace. Sphere thinks he knows everything.)
To use high-dimensional vectors, represent them as a column of numbers.
\[\left[\begin{array}{r}6.4\\3.0\\-2.5\\17.3\end{array}\right]\ \ \ \left[\begin{array}{r}-14.2\\-6.9\\18.0\\1.5\\-0.3\end{array}\right]\ \ \ \left[\begin{array}{r}5.3\\-9.6\\84.1\\5.7\\-11.3\\4.8\end{array}\right]\ \ \ \cdots\ \ \ \left.\left[\begin{array}{r}7.2\\-4.4\\0.6\\-4.1\\4.7\\\vdots\ \ \\-7.3\\8.3\end{array}\right]\right\} n\]
Sensible people may consider it mathematical ostentation to promote simple columns of numbers into vectors in high-dimensional space. But doing so lets us draw the analogy between data and familiar geometrical concepts: lengths, angles, alignment, etc. Operations that are mysterious as a long sequence of arithmetic steps become concrete when seen as geometry.
There is nothing science-fiction-like about so-called “high-dimensional” spaces; they don’t correspond to a physical place. Nevertheless, many-component vectors often appear in advanced physics. Famously, the Theory of Relativity involves 4-dimensional space-time. The vector representing the state of an ordinary particle contains the position and velocity, \((x, y, z, v_x, v_y, v_z)\), as well as angular velocity: nine dimensions. In statistics, engineering, and statistical mechanics, the term degrees of freedom is the preferred alternative to “dimension.” Another example: computer-controlled machine tools have 5 degrees of freedom (or more). There is a cutting tool with an \(x, y, z\) position and orientation. (If ever you start to freak out about the idea of a 10-dimensional space, close your eyes and remember that this is only shorthand for the set of arrays with ten elements.)
28.3 Geometry & arithmetic
Three mathematical tasks are essential to working with vectors:
- Measure the length of a vector.
- Measure the angle between two vectors.
- Create a new vector by scaling a vector. Scaling makes the new vector longer or shorter and may reverse the orientation.
We have simple geometrical tools for undertaking these tasks: a ruler measures length, and a protractor measures angles. Along with pen and paper, these tools let us draw new vectors of any specified length.
The geometrical perspective is helpful for many purposes, but often we need to work with vectors using computers. For this, we use the numerical representation of vectors.
This section introduces the arithmetic of vectors. With this arithmetic in hand, we can carry out the above three tasks (and more!) on vectors that consist of a column of numbers. And while we can’t import a ruler, protractor, or paper into high-dimensional space, arithmetic is easy to do, regardless of dimension.
To scale a vector \(\vec{w}\) means more or less to change the vector’s length. A good mental image for scaling sees the vector as a step or displacement in the direction of \(\vec{w}\). Scaling means to go on a simple walk, taking one step after the other in the same direction as the \(\vec{w}\). We write a scaled vector by placing a number in front of the name of the vector. \(3 \vec{w}\) is a short walk of three steps; \(117 \vec{w}\) is a considerably longer walk; \(-5 \vec{w}\) means to take five steps backward. You can also take fraction steps: \(0.5 \vec{w}\) is half a step, \(19.3 \vec{w}\) means to take 19 steps followed by a 30% step. Scaling a vector by \(-1\) means flipping the vector tip-for-tail; this does not change the length, just the orientation.
Arithmetically, scaling a vector is accomplished simply by multiplying each of the vector’s components by the same number. Two illustrate, consider vectors \(\vec{v}\) and \(\vec{w}\), each with \(n\) components. (We use \(\vdots\) to indicate components we haven’t bothered to write out.)
\[\vec{v} \equiv \left[\begin{array}{r}6\\2\\-4\\\vdots\\1\\8\end{array}\right]\ \ \ \ \ \ \ \ \ \ \ \ \vec{w} \equiv \left[\begin{array}{r}-3\\1\\-5\\\vdots\\2\\5\end{array}\right]\]
To scale a vector by 3 is accomplished by multiplying each component by 3
\[3\, \vec{v} = 3\left[\begin{array}{r}6\\2\\-4\\\vdots\\1\\8\end{array}\right] = \left[\begin{array}{r}18\\6\\-12\\\vdots\\3\\24\end{array}\right]\]
Vector scaling is perfectly ordinary multiplication applied component by component, that is, *** componentwise ***.
Scaling involves a number (the “scalar”) and a single vector. Other sorts of multiplication involve two or more vectors.
The dot product is one sort of multiplication of one vector with another. The dot product between \(\vec{v}\) and \(\vec{w}\) is written \[\vec{v} \bullet \vec{w}\].
The arithmetic of the dot product involves two steps:
- Multiply the two vectors componentwise. For instance:
\[\underset{\Large \vec{v}}{\left[\begin{array}{r}6\\2\\-4\\\vdots\\1\\8\end{array}\right]}\ \underset{\Large \vec{w}}{\left[\begin{array}{r}-3\\1\\-5\\\vdots\\2\\5\end{array}\right]} = \left[\begin{array}{r}-18\\2\\20\\\vdots\\2\\40 \end{array}\right]\]
- Sum the elements in the componentwise product. For the component-wise product of \(\vec{v}\) and \(\vec{w}\), this will be \(-18 + 2 + 20 + \cdots +2 + 40\). The resulting sum is an ordinary scalar quantity; a dot product takes two vectors as inputs and produces a scalar as an output.
R/mosaic provides a beginner-friendly function for computing a dot product. To mimic the use of the dot, as in \(\vec{v} \bullet \vec{w}\), the function will be invoked using infix notation. You have a lot of infix notation experience, even if you have never heard the term. Some examples:
3 + 2 7 / 4 6 - 2 9 * 3 2 ^ 4Infix notation is distinct from the functional notation that you are also familiar with, for instance sin(2) or makeFun(x^2 ~ x).
You can, if you like, invoke the +, -, *, /, and ^ operations using functional notation. Nobody does this because the commands are so ugly:
`+`(3, 2)## [1] 5
`/`(7, 4)## [1] 1.75
`-`(6, 2)## [1] 4
`*`(9, 3)## [1] 27
`^`(2, 4)## [1] 16
The R language makes it possible to define new infix operators, but there is a catch. The new operators must always have a name that begins and ends with the % symbol, for example, %>% or %*% or %dot%.
Here is an example of using %dot% to calculate the dot product of two vectors embedded in five-dimensional space:
a <- rbind(1, 2, 3, 5, 8, 13)
b <- rbind(1, 4, 2, 3, 2, -1)
a %dot% b
## [1] 33The vectors combined with %dot% must both have the same number of elements. Otherwise, an error message will result, as here:
rbind(2, 1) %dot% rbind(3, 4, 5)
## Error in rbind(2, 1) %dot% rbind(3, 4, 5): Vector <u> must have the same number of elements as vector <b>.We have not yet shown you the use of the dot product in applications. At this point, remember that a dot product is not ordinary multiplication but a two-stage operation of pairwise multiplication followed by summation.
28.4 Vector lengths
The arithmetic used to calculate the length of a vector is based on the Pythagorean theorem. For a vector \(\vec{u} = \left[\begin{array}{c}4\\3\end{array}\right]\) the vector is the hypotenuse of a right triangle with legs of length 4 and 3 respectively. Therefore, \[\|\vec{u}\| = \sqrt{4^2 + 3^2} = 5\ .\] For vectors with more than two components, follow the same pattern: sum the squares of the components, then take the square root.
Compute the length of a vector \(\vec{u}\) using the dot product:
\[\|\vec{u}\| = \sqrt{\strut\vec{u} \bullet \vec{u}}\ .\]
Although length has an obvious physical interpretation, in many areas of science, including statistics and quantum physics, the square length is a more fundamental quantity. The square length of \(\vec{u}\) is simply \(\|\vec{u}\|^2 = \vec{u}\bullet \vec{u}\).
Consider the two vectors
\[\vec{u} \equiv \left(\begin{array}{c}3\\4\end{array}\right) \ \ \ \mbox{and} \ \ \ \vec{w} \equiv \left(\begin{array}{c}1\\1\\1\\1\end{array}\right) \]
The length of \(\vec{u}\) is \(|| \vec{u} || = \sqrt{\strut 3^2 + 4^2} = \sqrt{\strut 25} = 5\).
The length of \(\vec{w}\) is \(|| \vec{w} || = \sqrt{\strut 1^2 + 1^2 + 1^2 + 1^2} = \sqrt{\strut 4} = 2\).
28.5 Angles
Any two vectors of the same dimension have an angle between them. Vectors have only two properties: length and direction. To find the angle between two vectors, pick up one vector and relocate its “tail” to meet the tail of the other vector.
Measure the angle between two vectors the short way round: between 0 and 180 degrees. Any larger angle, say 260 degrees, will be identified with its circular complement: 100 degrees is the complement of a 260-degree angle.
In 2- and 3-dimensional spaces, we can measure the angle between two vectors using a protractor: arrange the two vectors tail to tail, align the baseline of the protractor with one of the vectors and read off the angle marked by the second vector.
It is also possible to measure the angle using arithmetic. Suppose we have vectors \(\vec{v}\) and \(\vec{w}\) embedded in the same dimensional space. That is, \(\vec{v}\) and \(\vec{w}\) have the same number of components:
\[\vec{v} = \left[\begin{array}{c}v_1\\v_2\\\vdots\\v_n\\\end{array}\right]\ \ \ \text{and}\ \ \ \vec{w} = \left[\begin{array}{c}w_1\\w_2\\\vdots\\w_n\\\end{array}\right]\ ,\]
Using the dot-product and length notation, we can write the formula for the cosine of the angle between two vectors as
\[\cos(\theta) \equiv \frac{\vec{v}\cdot\vec{w}}{\|\vec{v}\|\ \|\vec{w}\|}\ .\]
Remember that the dot-product-based formula above gives the cosine of the angle between the two vectors. It turns out that in many applications, cosine is what’s needed. If you insist on knowing the angle \(\theta\) rather than \(\cos(\theta)\), the trigonometric function \(\arccos()\) will do the job. For instance, if \(\theta\) is such that \(\cos(\theta) = 0.6\), compute the angle in degrees with ::: {.cell layout-align=“center” fig.showtext=‘false’}
acos(0.6)*180/pi
## [1] 53.1301The trigonometric functions in R (and in most other languages) do calculations with angles in units of radians. Multiplication by 180/pi converts radians to degrees. Figure 28.4 shows a graph of converting \(\cos(\theta)\) to \(\theta\) in degrees.
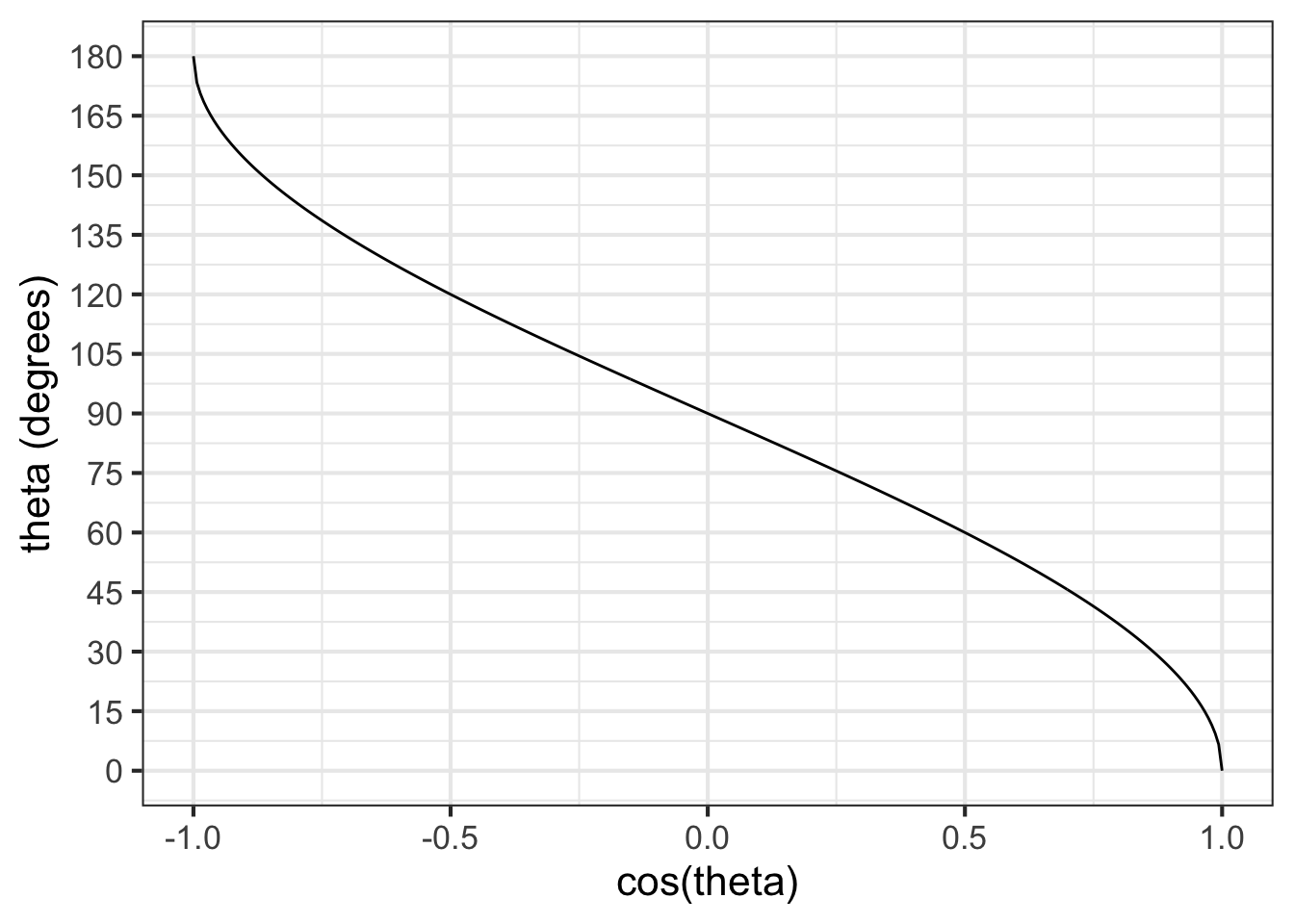
acos() in R) converts \(\cos(\theta)\) to \(\theta\).:::
28.6 Orthogonality
Two vectors are said to be orthogonal when the angle between them is 90 degrees. In everyday speech, we call a 90-degree angle a “right angle.” The word “orthogonal” is a literal translation of “right angle.” (The syllable “gon” indicates an angle, as in the five-angled pentagon or six-angled hexagon. “Ortho” means “right” or “correct,” as in “orthodox” (right beliefs) or “orthodontics” (right teeth) or “orthopedic” (right feet).)
Two vectors are at right angles—we prefer “orthogonal” since “right” has many meanings not related to angles—when the dot product between them is zero.
Find a vector that is orthogonal to \(\left[\strut\begin{array}{r}1\\2\end{array}\right]\).
The arithmetic trick is to reverse the order of the components and put a minus sign in front of one of them, so \(\left[\strut\begin{array}{r}-2\\1\end{array}\right]\).
We can confirm the orthogonality by calculating the dot product: \(\left[\begin{array}{c}-2\\\ 1\end{array}\right] \cdot \left[\strut\begin{array}{r}1\\2\end{array}\right] = -2\times1 + 1 \times 2 = 0\).
In R, write this as
u <- rbind( 1, 2)
v <- rbind(-2, 1)
u %dot% v
## [1] 0
Find a vector orthogonal to \(\left[\strut\begin{array}{r}1\\2\\3\end{array}\right]\).
We have a little more scope here. A simple approach is to insert a zero component in the new vector and then use the two-dimensional trick to fill in the remaining components.
For instance, starting with \(\left[\strut\begin{array}{r}0\\\_\\ \_\end{array}\right]\) the only non-zero components of the dot product will involve the 2 and 3 of the original vector. So \(\left[\strut\begin{array}{r}0\\ -3\\ 2\end{array}\right]\) is orthogonal. Or, if we start with \(\left[\strut\begin{array}{r}\_\\0\\\_\end{array}\right]\) we would construct \(\left[\strut\begin{array}{r}-3\\ 0\\ 1\end{array}\right]\).
28.7 Exercises
Exercise 28.01
Using these vectors $$
$$ calculate the length of each of these vectors. (Hint: Save yourself trouble by doing it in R.)
- \(2 \vec{u}\)
- \(- 2 \vec{u}\)
- \(4 \vec{u}\)
- \(17 \vec{v}\)
- \(- 1.5 \vec{w}\)
Exercise 28.03
Using R/mosaic and the %dot% and sqrt() functions, calculate the length of each of these vectors:
\[\vec{u} \equiv \left[\begin{array}{r}\ 35\\ -93\\ -99\end{array}\right]\ \ \ \vec{v} \equiv \left[\begin{array}{r} -59\\\ 41\\ -41\end{array}\right]\ \ \ \vec{w} \equiv \left[\begin{array}{r} -76\\ -71\\ -48\end{array}\right]\ \ \ \vec{x} \equiv \left[\begin{array}{r} -96\\\ 83\\\ 35\end{array}\right]\]
Exercise 28.05
Consider this vector
\[\vec{x} \equiv \left[\begin{array}{r}\ 470\\\ 210\\ -430\end{array}\right]\ .\]
For each of the following vectors, calculate the scalar multiplier \(\alpha\) such that \(\alpha \vec{x}\) equals the vectors. If there is no such multiplier, say why.
$$
$$
Hint: Try componentwise division.
Exercise 28.07
Here are four vectors.
\[\vec{u} \equiv \left[\begin{array}{r}\ 18\\\ 79\\\ 33\\ -41\end{array}\right]\ \ \ \vec{v} \equiv \left[\begin{array}{r} -35\\ -62\\ -32\\ -7\end{array}\right]\ \ \ \vec{w} \equiv \left[\begin{array}{r} -44\\\ 81\\\ 74\\ -4\end{array}\right]\ \ \ \vec{x} \equiv \left[\begin{array}{r} -9\\\ 71\\ -69\\\ 33\end{array}\right]\]
Which one of the above vectors is orthogonal to this one?
\[\vec{z} \equiv \left[\begin{array}{r} -1\\ -10\\\ 20\\\ 5\end{array}\right]\]
Exercise 28.09
A. Calculate the cosine of the angle between this vector
\[\vec{z} \equiv \left[\begin{array}{r} -1\\ -10\\\ 20\\\ 5\end{array}\right]\]
and each of the following vectors:
$$
$$
B. Translate each of the cosines from part (A) into degrees of the angle. (Rounding to the nearest degree is fine.)
Exercise 28.11
Consider this set of vectors
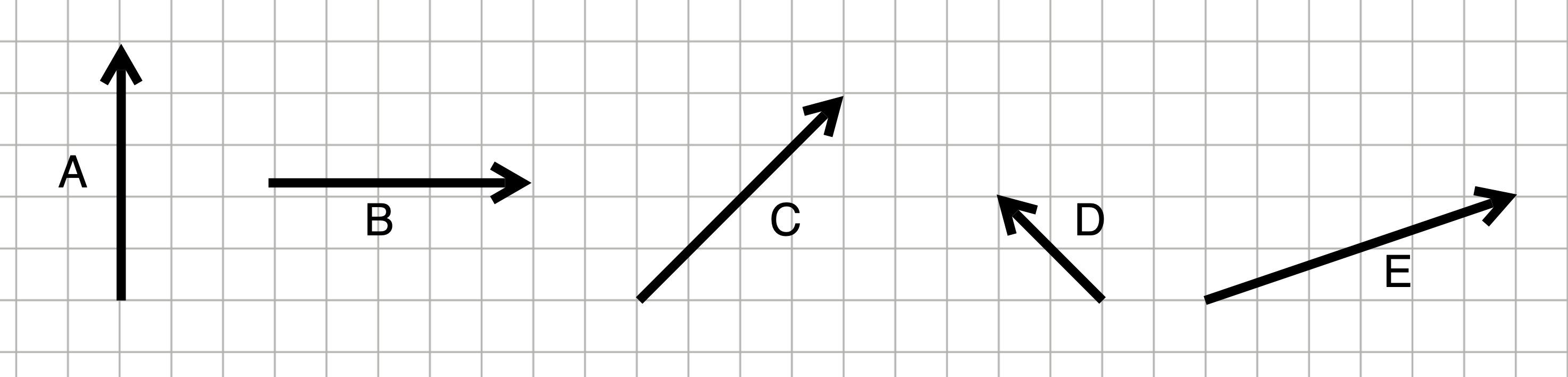
Find the lengths of each of these vectors. Assume that the vectors begin and end exactly on the graph-paper intersections.
Two pairs of vectors in this set are orthogonal. Which ones?
Just using your eye, say whether the dot product between every pair of vectors is positive, zero, or negative.
- A & B
- A & C
- A & D
- A & E
- B & C
- B & D
- B & E
- C & D
- C & E
- D & E
Exercise 28.13
Here are several vectors:
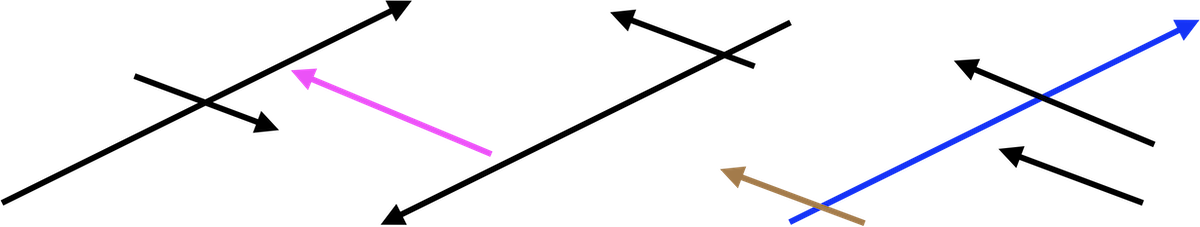
- Remembering that mathematical vectors have only two properties—length and direction—how many different mathematical vectors are being shown.
Measure the length of each vector. (Hint: Use a ruler! You can round to the nearest millimeter.)
Find the included angle between the \(\color{blue}{\text{blue}}\) and \(\color{brown}{\text{brown}}\) vectors. (Your answer should be correct to within \(\pm 15^\circ\).)
- Find the included angle between the \(\color{magenta}{\text{magenta}}\) and \(\color{blue}{\text{blue}}\) vectors.
- Find the included angle between 0.7 times the \(\color{blue}{\text{blue}}\) vector and -11.3 times the \(\color{brown}{\text{brown}}\).
Exercise 28.15
Collision course?
Consider the diagram showing two straight-line tracks, a dot on each track, and a vector.
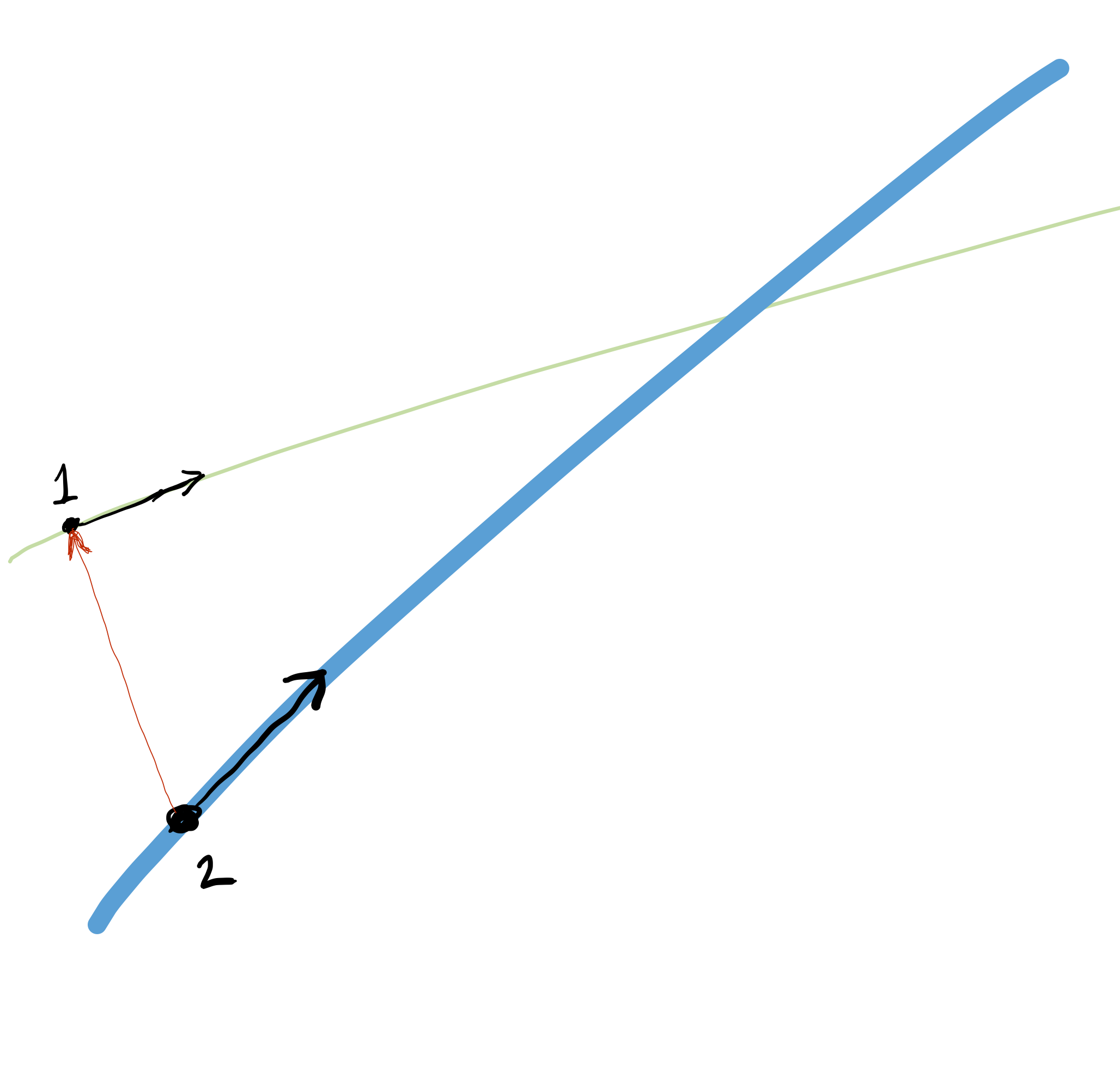
Let’s imagine that dot 1 is an aircraft and that the black vector attached to it is the aircraft’s velocity. We will call this \(\vec{v}_1\), Similarly for dot 2, where the velocity vector will be called \(\vec{v}_2\).
There is a third vector drawn in red: the difference in position of the two aircraft at the exact moment depicted in the drawing.
The question we want to address is whether the aircraft are on a collision course. Obviously, the two courses cross. So we know that the two aircraft will cross the same point. For a collision, the aircraft have to cross that point at the same time.
Copy over the drawing to your own piece of paper. You don’t need to get the vectors and positions exactly right; any reasonable approximation will do.
Now you will do visual vector addition and subtraction to answer the collision question.
The relative velocity of the two planes is the difference between their velocities. Subtract \(\vec{v}_2\) from \(\vec{v}_1\) and draw the resulting vector. Pay attention to both the length and direction of the relative velocity.
The displacement between the two planes is the red vector: the position of dot 2 subtracted from dot 1. Compare the directions of the relative velocity vector and the displacement vector. If they are aligned, then the planes are on a collision course.
In the picture as drawn, the relative velocity vector and the displacement vector are not aligned. Figure out how much you would need to change the length of \(\vec{v}_2\) so that the relative velocity does align with the displacement. (Keep the direction the same.) Draw this new vector and label it “vector for intercept.”
In (3) you changed the length of \(\vec{v}_2\) keeping the direction the same. Now you will keep \(\vec{v}_2\) at the original length, but change its direction so that the new relative velocity is aligned with the displacement vector.
Items (3) and (4) are two different ways of designing an intercept of plane 1 by plane 2.
Bonus) You can figure out how long it takes for each plane to reach the intersection point by finding out how many multiples of the velocity vector will cover the line segment between the plane’s position and the intersection point. For example, in the original drawing \(4 \vec{v}_1\) will bring the plane to the intersection point, so it takes 4 “time units” for the plane to reach the point. (What is the time unit? If velocity is in miles/hour, then the time unit is hours. If the velocity is in feet/second, then the time unit is seconds.) Your task: Figure out where aircraft 2 will be in 4 time units. This will tell you the separation between aircraft 2 and aircraft 1 when 1 reaches the intersection point. Draw and label this vector.
Exercise 28.17
In physics and engineering, there is a very important operation called the cross product and written \(\vec{u}\times\vec{v}\). The operation is only defined for vectors in 3-dimensional space. The output of the cross product is another 3-dimensional vector which can be calculated arithmetically as:
\[\left(\begin{array}{c}a\\b\\c\end{array}\right) \times \left(\begin{array}{c}e\\f\\g\end{array}\right) \equiv \left(\begin{array}{c}b\, g - c\, f\\c\, e - a\, g\\a\, f - b\, e\end{array}\right)\]
Make up coordinates for two three-dimensional vectors \(\vec{u}\) and \(\vec{v}\) that point in different directions.
Calculate the cross product \(\vec{w} \equiv \vec{u} \times \vec{v}\).
- Find the angle between \(\vec{w}\) and \(\vec{u}\).
- Find the angle between \(\vec{w}\) and \(\vec{v}\).
Other than this brief description, we will not use cross products at all in this course. But keep them in mind for your upcoming physics and engineering courses.