MOSAIC Calculus
Preface
Welcome to calculus
Calculus is the set of concepts and techniques that form the mathematical basis for dealing with motion, growth, decay, and oscillation. The phenomena can be as simple as a ball arcing ballistically through the air or as complex as turbulent airflow over a wing generating lift. Calculus is used in biology and business, chemistry, physics and engineering. It is the foundation for weather prediction and understanding climate change. It is the basis for the algorithms for heart rate and blood oxygen measurement by wristwatches. It is a key part of the language of science. The electron orbitals of chemistry, the stresses of bones and beams, and the business cycle of recession and rebound are all understood primarily through calculus.
Calculus has been central to science from the very beginnings. It is no coincidence that the scientific method was introduced and the language of calculus was invented by the same small group of people during the historical period known as the Enlightenment in the late 17th century. Learning calculus has always been a badge of honor and an entry ticket to professions. Millions of students’ career ambitions have been enhanced by passing a calculus course or thwarted by lack of access to one.
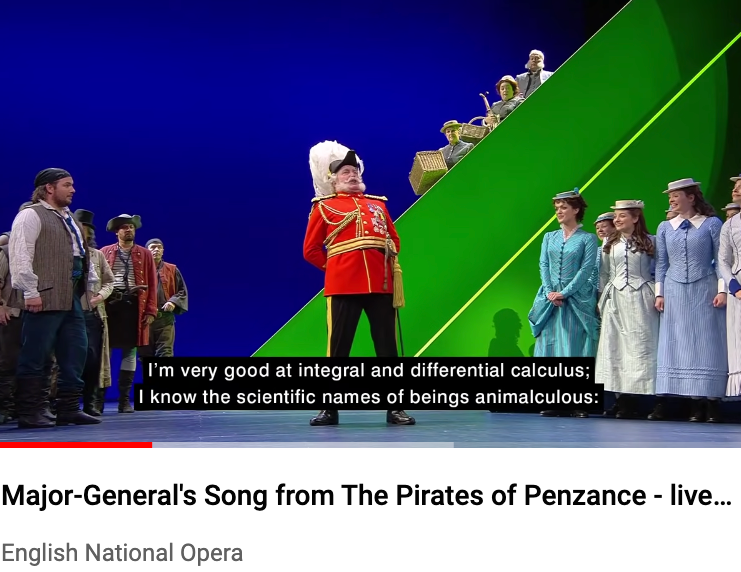
In the 1880s, a hit musical featured “the very model of a modern major general.” One of his claims for modernity: “I’m very good at integral and differential calculus.”
What was modern in 1880 is not modern anymore. Yet, amazingly, calculus today is every bit as central to science and technology as it ever. Indeed, calculus remains central to fields that were not even imagined in 1880, such as logistics, economics, and data science. One reason is that science, engineering, and society have now fully adopted the computer for almost all aspects of work, study, and life. The collection and use of data is growing dramatically. Machine learning has become the way human decision makers interact with such data.
Think about what it means to become “computerized.” To take an everyday example, consider video. Over the span of a human life, we moved from a system which involved people going to theaters to watch the shadows recorded on cellulose film to the distribution over the airwaves by low-resolution television, to the introduction of high-def broadcast video, to on demand streaming from huge libraries of movies. Just about anyone can record, edit, and distribute their own video. The range of topics (including calculus) on which you can access a video tutorial or demonstration is incredibly vast. All of this recent progress is owed to computers.
The “stuff” on which computers operate, transform, and transmit is always mathematical representations stored as bits. The creation of mathematical representations of objects and events in the real world is essential to every task of any sort that any computer performs. Calculus is a key component of inventing and using such representations.
You may be scratching your head. If calculus is so important, why is it that many of your friends who took calculus came away wondering what it is for? What’s so important about “slopes” and “areas” and how come your high-school teacher might have had trouble telling you what calculus is for?
The disconnect between the enthusiasm expressed in the preceding paragraphs and the lived experience of students is very real. There are two major reasons for that disconnect, both of which we tackle head-on in this book.
First, teachers of mathematics have a deep respect for tradition. Such respect has its merits, but the result is that almost all calculus is taught using methods that were appropriate for the era of paper and pencil—not for the computer era. As you will see, in this book we express the concepts of calculus in a way that carries directly over to the uses of calculus on computers and in genuine work.
Second, the uses of calculus are enabled not by the topics of Calc I and Calc II alone, but the courses for which Calc I/II are preliminary: linear algebra and dynamics. Only a small fraction of students who start in Calc I ever reach the parts of calculus that are the most useful. Fortunately, there is a large amount of bloat and rote in the standard textbook topics of Calc I/II. This can be removed to make room for the more important topics, as we try to do in this book.
You will want to use a computer to follow this book. Your instructor might want you to set up the required software in a way that fits the resources and course-support systems of your institution. Alternatively, you can set up what you need for free on a standard laptop computer or even use a tablet with a keyboard. Instructions for this are given in Appendix ?sec-software-installation.
The computer language used in this book is R. This is a mainstream language in high demand by employers in many field. The small amount of R that you need to learn for this book will open doors to much greater possibilities. We have augmented R with a widely used package, {mosaic}, that simplifies access to calculus-related operations.
Instructor’s preface
The “MOSAIC” in the book’s title refers to a movement in undergraduate mathematics to integrate Modeling, Statistics and data science, Computing, and Calculus. Skill in all these areas is needed for successful work in the technical and scientific world. Traditionally, teaching does not honor the strong links among these areas and ignores the advantages of teaching them in a unified way. Indeed, modeling, though often mentioned in calculus textbook blurbs, is hardly taught at all. Introductory statistics courses, even those with a formal pre-requisite of calculus, do not draw on calculus concepts beyond the mention of “area under a curve.” Few and far between are introductory computing courses that reinforce calculus and statistics topics, or calculus courses that develop and build on computing and data skills.
The isolation of mathematical calculus from disciplines that ought to be considered allies leads to a devastating gap in the education of students. The half-life of a student in a calculus sequence is, roughly speaking, one course. (The decay in participation starts in algebra and trigonometry.) The result is that only a small fraction of students see relevant mathematics of multiple variables and hardly any encounter the powerful concepts of spaces, vectors, and matrix factorizations traditionally reserved for a junior-year linear algebra course. Contemporary statistical modeling techniques, including machine learning, draw heavily on a small core of linear-algebra topics.
The design of the mosaic serves the goal of providing for all students access to a broad, directly useful education in the mathematical sciences. One component of access is keeping the program small enough to fit in with a plausible student schedule. Our working definition of “small enough” is one-quarter of the first two years of university. Fitting within this envelope, students ought to achieve basic competence in computing, statistics, and calculus.
Calculus provides opportunities to prepare students well for both modern statistics and computing. The most direct ties to statistics are modeling, functions of multiple variables, and concepts of linear spaces. The relevant links of calculus to computing are extensive and go both ways. To give but one example: It’s impractical for students to construct contour plots without a computer. With a computer at hand, students can learn about mathematical ideas such as gradients and iterative optimization. For instance, constrained optimization is hardly a topic of standard introductory calculus and Lagrange multipliers are mysterious even to many professors. The essential concepts become much clearer when they can be presented using graphical tools of contours and gradient fields.
A book that attempts to build on the connections among historically distinct disciplines must also resolve inconsistencies in nomenclature and notation. We draw the instructor’s attention to some of these and the policies adopted in the book:
Variable. In mathematics “variable” is used with many different reasons, in computing “variable” is used colloquially to mean “the name of an object,” and in statistics a “variable” refers to data: a column of a data frame or, more generally, a specific attribute of the units of observation that form the rows of the data frame. (See Section 7.1 for definitions of “data frame” and “unit of observation.”) We reserve “variable” to be used in the statistical sense. Consequently, a “function of several variables” becomes a “function with several inputs.”
Output. Evaluating a function, either a mathematically or on a computer, produces an output. Functions take inputs and produce outputs. Typical names for inputs are, following tradition, the last few letters of the alphabet: \(t, u, v, w, x, y, z\).
Function names. Functions always have a name. \(f()\), \(g()\), \(h()\) are the pronouns for discussing functions in general, but in specific applications functions often have more descriptive names, e.g. population() or elev() or risk(). The empty parentheses are a reminder that the thing being named is a function and not an input or parameter. Since \(y\) is used as an input name, we never use it for the name of a function or to identify the output of a function. So, \(y=mx+b\) is not an esteemed phrase in this book. Instead, when we want to define a straight-line function we write \(g(x) \equiv a x + b\) or some other parameterization, for instance \(g(x) \equiv a (x - x_0)\).
Special inputs. Often, a problem or application context requires the identification of some special values for inputs to a function, for instance, argmaxes or zero crossings or starting time. These are often constructed by using an output name (often \(t\) through \(z\)) with a subscript or a non-numerical superscript as in \(y^\star\).
Output (part 2). When we mean something like “the output of the function \(f()\) at its argmax,” we write \(f(x_\star)\), or something similar. When we mean, “the output of function \(f()\) at some as yet unspecified input,” we write, naturally enough, \(f(x)\).
Formulas. An expression like \(ax + b\) is a formula. One of the most common ways to define a function is by using a formula. But creating a function from a formula requires some special syntax, as demonstrated earlier with \(g(x) \equiv a x + b\). The names used within the parentheses on the left side of \(\equiv\) are the input names. Other symbols in the formula are called parameters.
Tilde expression. We use the R language in this book. Those familiar with R know that there is a special kind of expression called a “formula,” for instance
a*x + b ~ x. One of the main uses for R formulas is to represent a mathematical formula when creating a function. “Formulas representing formulas” can lead to confusion. We address this by violating the technical vocabulary of R and calling an expression likea*x + b ~ xa “tilde expression.” This name properly draws attention to the ~ (“tilde”) character that is an essential component to R-language formulas. A typical use for a tilde expression is to create a computer version of a function. The computer version of \(g(x) \equiv a x + b\) isg <- makeFun(a*x + b ~ x). In this use, the~ xpart of the tilde expression identifies the input name, just as does the \(x\) in \(g(x) \equiv ...\). You’ll also use tilde expressions for graphics and operations such as differentiation and anti-differentiation.
Those familiar with R may be tempted to use the native function-building syntax, which looks like
g <- function(x, a, b) {
a*x + b
}We strongly encourage you to use makeFun() instead. One reason is to reinforce the use of tilde expressions which are needed to identify the “with-respect-to” input in differentiation and anti-differentiation, as well as the frame of a graph. Another reason has to do with rules of scoping in computer languages, which have no obvious analog in mathematical notation. We prefer to leave scoping to a computer science class, rather than making it a pre-requisite for calculus. makeFun() avoids the scoping difficulties.
- Differential notation. Historically, Leibniz’s lovely ratio notation, for instance, \[\frac{dy}{dx}\ ,\] helped generations of students learn differential calculus and see the connections to integral calculus. It is, however, wordy, which is why other notations—\(f'\) or \(\dot{x}\) or \(f^{(1)}\) so often appear. But Leibniz could hardly have anticipated a future in which writing is done mainly with keyboards and linear sequences of characters. There is no mainstream computer language in which
df/dxorf'or\dot{x}orf^{(1)}are valid names. To simplify the use of the computer, we use \(\partial_x y\) notation for differentiation. This can be easily morphed into a legal computer name:dx_y. We use \(\partial\) instead of the Latin \(d\), partly to mark differentiation as something special and partly because we will use notation like \(\partial_{xt} g\) when dealing with functions of multiple variables, or \(\partial_{xx} f\) for second derivatives.
The book is designed to support six to eight credit hours of calculus study. The algebra pre-requisites are kept to a minimum, trigonometry beyond sines and cosines is not needed. In the starting “Preliminaries” part of the book nine “pattern-book” algebraic functions are introduced that form the basis for modeling work. “Preliminaries” also introduces computing notation, particularly that used for graphing functions.
“Modeling,” Block I, introduces topics that are essential to the rest of the book and is worth spending considerable class time on regardless of the previous experience of students. Block II, “Differentiation,” is self-explanatory to a calculus instructor. Absence of extensive drill on symbolic differentiation of obscure functions or the use of Taylor polynomials or l’Hopital’s rule to provide even more drill is entirely intentional. Much more important that students master differentiation of the nine pattern-book functions and their parameterized version.
Block III, “Vectors and linear combinations,” does not depend on previously covering differentiation. The sequence Preliminaries-Modeling-Vectors could make a suitable 3- or 4-credit course for students entering data science. Block III might have been reasonably titled “Linear algebra.” But the universal emphasis on determinants and inverses of square matrices in a conventional linear algebra course is not a suitable introduction for working with data, and we did not want to suggest that all the conventional topics of linear algebra are included.
Block IV, “Accumulation,” builds on Block II, where differentiation is treated less as an algebraic process than as a relationship between functions. Our focus is on occasions when anti-differentiation is a useful modeling tool for extracting certain forms of information from a function. Instructors are advised to minimize or wholly avoid the area-under-a-curve metaphor. Like cigarettes, that metaphor is addictive and creates dis-ease with the more important roles for accumulation in contexts like dynamics. The final chapter of Block IV is about symbolic integration of functions constructed from from the pattern-book. Including it is a concession to administrative practices at universities where topics like “integration by parts” are included in hard-to-change course-catalog copy. Those techniques are not used elsewhere in the book.
Block V, “Dynamics,” introduces systems, that is, wholes made of multiple connected parts. Although the context used is differential equations, techniques for finding solutions are not central. More important are the phenomena (e.g. oscillation), the opportunities for modeling and showing how simple mathematical models can provide insight to otherwise seemingly complex natural and social systems, extension of the linear-algebra material from Block III to eigenvalues and eigenvectors, and a glimpse at the surprisingly close connection between exponentials and sinusoids.
The last block, “Manifestations,” is arranged along different lines than the previous chapters. The point is to show how calculus operations show themselves in a wide variety of contexts. We are not making up opportunities for more drill in symbolic differentiation and anti-differentiation. In the “Probability” chapter, to give an example, what’s central is the relationships between functions. One of these relationships is standard in calculus books, that between what’s called the CDF and the PDF. Less basic and not at all standard, the relationship between prior, likelihood, and posterior functions. It is not required to cover all the chapters in “Manifestations.” They do not much depend one on the other. Choose the ones that are best suited to the directions in which your students are heading. And the topics need not be delayed to the end of the course. For instance, the constrained optimization topic in “Optimization” can be handled with the material up to Block IV.
Many highly expert calculus instructors have taught with these materials. Some of their experiences may be relevant to instructors who haven’t yet used MOSAIC Calculus. First, the experts are surprised by how many esteemed, traditional calculus topics are given short shrift or even omitted altogether, and even more surprised that their exclusion does not diminish the course. Second, many experts find that the calculus in this book is not calculus as they have been trained to think about it, but that nonetheless “it works.” Third, instructors who try to avoid spending class time on the computational elements of the book find that their students echo the avoidance. As these instructors go through their first year, they discover that there are only a handful of computational patterns (e.g. tilde expressions, domains) and that students would have avoided many headaches by facing them head-on from the start of the course. Some advice: Don’t think that you have to learn R before you can master using R to teach this book. The mosaic software that powers this book is a better place to start than with the many more general introductions and tutorials on R computing available in printed and video form.
Most universally, even the expert instructors find they are unfamiliar with tranches of the material. Leading examples are dimensions of measurement, splines, mechanics (e.g. torque), the uses of orthogonalization, and, broadly, dynamics. Teaching unfamiliar material is admittedly stressful, but highly beneficial to yourself and your students. Dimensions and units, in particular, are a great guide to thinking; take every opportunity to ask your class what are the dimensions of the inputs to and outputs from a function and whether an operation makes sense in terms of dimensions. Consistently, the experts find that thinking about physical dimension gives them unexpected insight into the tasks and methods of calculus.
- Daniel Kaplan, Saint Paul, Minnesota, July 2022
Acknowledements
This project was initiated by the Mathematical Sciences department at the US Air Force Academy. They recognized that a traditional calculus introduction is ill-suited to the needs of STEM in the 21st century.
Critical support was given by the ARDI Foundation which awarded the Holland H. Coors Chair in Education Technology to one of the project members, Daniel Kaplan. This made possible a year-long residency at USAFA during which time he was able to work unhindered on this project.
Macalester College, where Kaplan is DeWitt Wallace Professor of Mathematics, Statistics, and Computer science, was the site where the overall framework and many of the materials for a STEM-oriented calculus were developed. Particularly important in the germination were David Bressoud and Jan Serie, respectively chairs of the Macalester math and biology departments, as well as Prof. Thomas Halverson and Prof. Karen Saxe, who volunteered to team teach with Kaplan the first prototype course. Early grant support from the Howard Hughes Medical Foundation and the Keck Foundation provided the resources to carry the prototype course to a point of development where it became the entryway to calculus for Macalester students.
Profs. Randall Pruim (Calvin University) and Nicholas Horton (Amherst College) were essential collaborators in developing software to support calculus in R. They and Kaplan formed the core team of Project MOSAIC, which was supported by the US National Science Foundation (NSF DUE-0920350).
Joel Kilty and Alex McAllister at Centre College admired the Macalester course and devoted much work and ingenuity to write a textbook, Mathematical Modeling and Applied Calculus (Oxford Univ. Press), implementing their own version. Their textbook enabled us to reduce the use of sketchy notes in the first offering of this course at USAFA.